데이터의 저장방식

컴퓨터에서 정수(integer)와 부동소수점(floating) 등의 정보가 저장되고 표현되는 기본적인 방식을 메모했습니다.

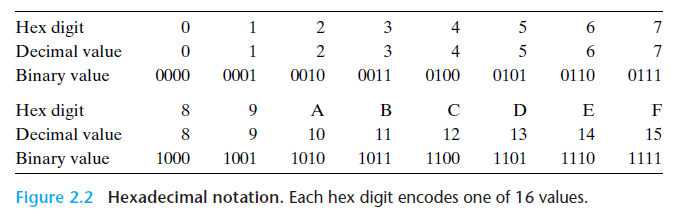
  • 16진수를 알아둬야 편합니다. 아래 표와 같습니다. hexadecimal-notation
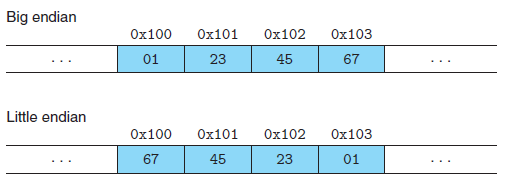
  • big endian, little endian 표현법이 있습니다. 메모리 주소에 따라 데이터가 저장되는데, big endian은 낮은 주소, 즉 데이터가 시작하는 부분에 큰 단위가 있고 little endian은 그 반대로 낮은 주소에 작은 단위가 있습니다. big-endian-little-endian

정수 - 2의 보수(Two’s Complement)

2의 보수란 컴퓨터의 정수 표현 방식입니다. 가령 4비트 데이터인 0110은 10진수 6이 됩니다.

  • 정수는 부호(Signed)/양수(Unsigned) 두 가지로 해석할 수 있습니다.
  • 연산 중 overflow가 있을 수 있습니다. 가령 32비트 정수에서 가장 큰 수는 $2^31 -1 = 247483647$ 인데, 16진수로는 0x7fffffff로 표현됩니다. 여기에 1을 더하면 0x80000000이 됩니다. 이는 32비트로 표현 가능한 가장 작은 음수(-2147483648)가 됩니다.
  • 역사적으로 1의 보수 등의 방법이 있었으나 비효율적이어서 사장되었습니다.

실수 - 부동소수점(Floating Point)

부동소수점이란 컴퓨터의 실수 표현 방식입니다. 32비트로 실수를 나타내면 single-precision, 64비트로 실수를 나타내면 double-precision이라고 합니다.

  • 구성 요소
    • sign. 부호를 나타내는데, 1이면 음수이고 0이면 양수를 뜻합니다.
    • exponent. 지수 부분이라고 번역됩니다.
    • significand. 가수 부분이라고 번역되는데, fraction 혹은 mantissa라고도 부릅니다. 1과 2 사이, 혹은 0과 1사이를 표현하는 데에 사용됩니다.
    • 32비트 실수의 경우 sign 1비트 + exponent 8비트 + significand 23비트로 구성됩니다.
    • 64비트 실수의 경우 sign 1비트 + exponent 11비트 + significand 52비트로 구성됩니다.
    • 부동소수점 표현은 지수 부분이 무엇인지에 따라 4가지로 분류됩니다. Normalized, Denormalized, Infinity, NaN(Not a Number)입니다.
      • Normalized 값은 지수 부분 $E$를 $E = e - Bias$ 로 해석합니다. $e$는 지수 부분 비트열이 나타내는 unsigned number이고, Bias는 $2^k-1$ 값입니다 $k$는 지수 부분의 길이(32비트 실수면 8, 64비트 실수면 11)를 나타냅니다.
      • Denormalized 값은 지수 부분이 몽땅 0일 때를 말합니다. 지수 부분 값은 $E = 1 - Bias$ 로 해석합니다.
      • 지수 부분이 모두 1이면 특별한 경우입니다. 가수 부분이 모두 0이면 무한대, 그렇지 않으면 NaN을 나타냅니다.
    • 좀 더 쉽게 8비트 부동소수점으로 예시를 들 수 있습니다. 가령 8비트 중 첫 비트는 sign이고, 그 다음 4비트는 exponent, 그 다음 3비트는 significand(fractional part)라고 한다면 각 수는 다음과 같이 나타낼 수 있습니다.
      • 0: 0 0000 000. 지수 부분이 0000이므로 denormalized 값입니다.
      • 1/512: 0 0000 001. 지수 부분이 0000이므로 마찬가지로 denormalized 값이고, 8비트 부동소수점으로 나타낼 수 있는 양수 중에서는 가장 작은 값입니다.
      • 1/64: 0 0001 000. 지수 부분이 0000도 아니고 1111도 아니므로 normalized 값입니다. normalized 값 중에서는 가장 작은 값을 나타냅니다.
      • $\infty$: 0 1111 000는 양의 무한대를 나타냅니다. 1 1111 000은 음의 무한대입니다.
  • 정확도 문제가 있습니다. 가령 $\pi$의 값을 정확하게 계산하기 위해서는 다른 방법이 도입됩니다. 정수로 변환할 때도 정확도 문제가 있을 수 있습니다.

질문답변

  1. little endian과 big endian의 차이점은 무엇인가요?
    • 낮은 주소값(시작점)에 큰 단위가 나오면 big endian이고 작은 단위가 나오면 little endian 입니다.
  2. 2의 보수로 32bit signed integer를 나타낸다면 표현 가능한 양의 정수 최댓값은 얼마인가요? 그리고 그걸 16진수 표현법으로는 어떻게 나타내나요?
    • $2^31 - 1$, 즉 2147483647입니다. 16진수 표현법으로는 0x7fffffff로 나타냅니다.
  3. 32비트 부동소수점으로 0 11111111 00000000000000000000000은 얼마를 나타낼까요?
    • 지수 부분이 모두 1이고, 가수 부분이 모두 0이므로 무한대를 나타냅니다.